Wirklich keine Kritik! Vielmehr ein Denkanstoß zur vierten Dimension aus meinem geometrischen Verständnis soll das jetzt sein. Ich meine, man kann kein vierdimensionales Gebilde zweidimensional darstellen. Trotzdem ein Versuch von mir (nicht schön - nur zur Erklärung):
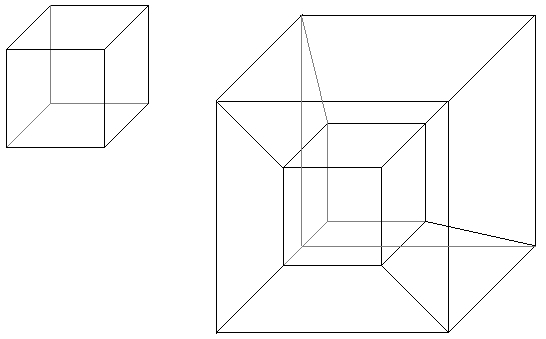
Aus einem zweidimensionalen Quadrat machen wir (besser wäre es mit Fluchtpunkt) etwas dreidimensionales, einen Würfel. Wir täuschen also mit nichtrechtwinkligen Vierecken eine Tiefe als dritte Dimension vor. Dabei wissen wir, dass alle Kanten in Wirklichkeit gleich lang und im rechten Winkel zueinander sind.
Wollten wir nun, genauso, wie wir aus sechs Quadraten einen Würfel gemacht haben, ein aus Würfeln gebildetes vierdimensionales "Etwas" zeichnen, müssten wir nun schiefwinklig im Raum arbeiten.
Ich habe rechts versucht ein 4D-"Etwas" zu zeichnen, dass acht Würfeln besteht (einer außen, einer innen und sechs Verbindungswürfel der Flächen). Wir müssten uns jetzt vorstellen, dass alle Kanten gleich lang seien und überall nur rechte Winkel vorgefunden werden.
Keine Angst, wenn ihr das nicht könnt, ich tu es auch nicht.
Vielleicht haben Bilder von Escher mit seinen konsequenten Perspektivefehlern etwas künstlerisches mit der vierten Dimension zu tun?
Es wird oft von der Zeit behauptet, sie sei die vierte Dimension. Darüber kann man in der Mathematik geteilter Meinung sein. In der Physik rechnet man schon fest mit 11 Dimensionen, womöglich noch mehr. Wer will da noch jeder Dimension eine fortlaufende Nummer geben?